注:本文更新于2023/12/27,修改了某些错误
前言
我也是服了,这篇文章写的高血压快出来了…🤔
本文注重理论,基本上不会有代码,理解起来比较麻烦,所以(将就着看吧)
不过,我写文章的风格是特别的傻瓜式,基本上小学生也能看懂罢?
多叉树
多叉树是什么?

规则:
- 每个节点有零个或多个子节点。
- 没有父节点的节点称为根节点。
- 每一个非根节点有且只有一个父节点。
- 除了根节点外,每个子节点可以分成一个或多个不相交的子树。
- 树中分叉最多的节点有几个分支,就称为几叉树。
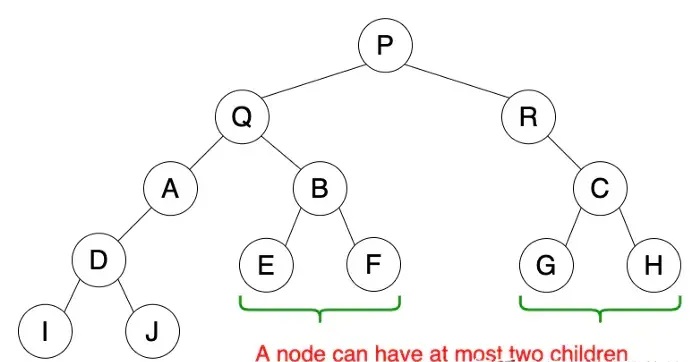
好好好,我知道给你一堆理论可能不理解,我详细的结合上面那张图解释一下(下面所有内容都围绕这张图介绍哦)
根
首先,最上方的节点(A),称为根节点或树根(root)
父子节点关系
关于父子节点,我举一些例子,大家理解一下
A称为B、C、D的父节点;B、C、D是A的子节点。
B称为E、F的父节点;E、F是B的子节点。
层数不相邻,不能称为父子节点关系。(如A、F)
没有连接,不能称为父子节点关系。(如C、F)
子树
树中的B节点是根节点的子节点,B和它的所有后代(E、F、I)也组成了一个树,称为这棵树的子树
同理,D节点和它的所有后代也称为这棵树的子树。为了方便表示,称它为D树。
G节点是D的子节点,G节点和它的所有后代称为D树的子树,即G树是D树的子树。
需要注意的是,一个树可能只有一个节点,C树也是A树的子树。
命名
分叉最多的节点有几个分支,就称为几叉树。
比如这个,分支最多的是A节点(3个),所以称为三叉树
二叉排序树
规则:
- 每个父节点最多有两个子节点(必须为二叉树)。
- 左子树中所有节点的值都小于左子树的父节点的值。
- 右子树中所有节点的值都大于右子树的父节点的值。
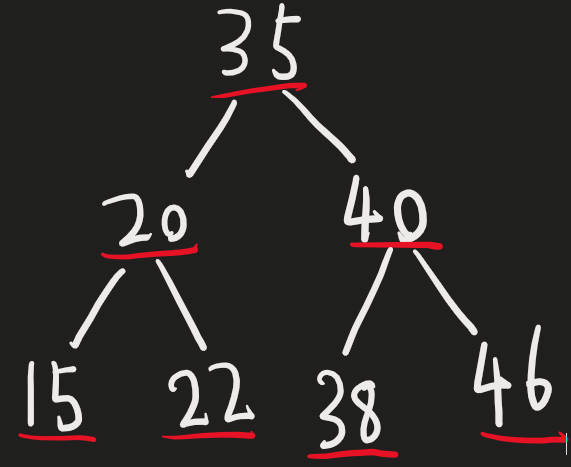
接下来,我还是借助这张图讲一下。
找一下规律,会发现:
左子节点的值都比父节点的值小
例如15<20,20<35,38<40(从左往右)
右子节点的值都比父节点的值大
例如22>20,40>35,46>40(从左往右)
但是~我们忽略了一个问题哦,我们只看到了个体而忽略了整体(子树,即子树中所有节点的值的和要大于/小于父节点)
所以,同理,整合一下,可以得到
左子树中所有节点的值都小于左子树的父节点的值。(20+15+22=35)
右子树中所有节点的值都大于右子树的父节点的值。(40+38+46>35)
好啦,树形结构这部分就ok了
深度优先搜索(DFS)
何为深度优先搜索?
深度优先搜索通过先访问根节点,然后递归地访问左子树和右子树的方式进行遍历。具体来说,深度优先搜索使用栈(可以是显式的数据结构,也可以是递归的函数调用栈)来保存待访问的节点。
说人话就是:
尽可能深地搜索树的分支。(不撞南墙不回头)
对于每个节点,优先搜索它的左子节点,再搜索它的右子节点。

所以,按照图中箭头的顺序:A -> B -> D -> E -> F -> G-> C
代码
主要还是用到递归
a = []
def dfs(node):
a.append(node.value)
# 该节点有左子节点,则搜索左子节点(终止条件)
if node.left_child != None:
dfs(node.left_child)
# 该节点有右子节点,则搜索右子节点(终止条件)
if node.right_child != None:
dfs(node.right_child)广度优先搜索(BFS)
原理
从第一层开始,从左到右搜索完该层所有节点后,再搜索下一层。

1→2→3→4→5→6→7
代码
要想实现,需要用到队列
(忘了的朋友可以看看之前发的文章哦~python中的队列与栈)
思路(还是按照上图)
- 第一层只有根节点,直接搜索即可
- 搜索第二层时,依次搜索节点1的左子节点(2,node1.left_child)、右子节点(3,node1.right_child)
- 搜索第三层时,先搜索节点2的左子节点(4,node2.left_child)、右子节点(5,node2.left_child)
- 搜索第三层时,再搜索节点3的左子节点(6,node3.left_child)、右子节点(7,node3.left_child)
我们发现,下一层的搜索顺序依赖于上一层的搜索顺序;所以搜索每一层的节点时,借助容器(队列)将它们的子节点暂时存储下来。
整理一下
先将根节点放入队列中。
如果队列不为空:
- 取出队列中的第一个元素,然后查看该元素的值
- 如果当前节点值等于目标节点值,就结束搜索
- 如果该元素有左子节点,则将左子节点放入队列中
- 如果该元素有右子节点,则将右子节点放入队列中
from queue import Queue
def bfs(node):
q = Queue() # 创建一个队列用于存储待访问的节点
q.put(node) # 将根节点放入队列
while q.qsize() != 0: # 当队列非空时
node = q.get() # 从队列中取出一个节点
print(node.value) # 访问当前节点的值
if node.value == 2: # 如果当前节点的值为2(目标值),结束搜索
return
if node.left_child: # 如果当前节点有左子节点,则将左子节点放入队列
q.put(node.left_child)
if node.right_child: # 如果当前节点有右子节点,则将右子节点放入队列
q.put(node.right_child)
结束喽
好吧,本篇文章就写到这儿,我也不知道怎么结尾了hhh
(写5篇文章的flag完成度:2/5)





写的很奈斯,特来拜访博主
谢谢!ヾ(´・ ・`。)ノ”